শিরোনামটা দেখলে কেমন একটু ধাঁধা লেগে যায়, তাই না? ছিল বেড়াল, হয়ে গেল রুমালের মতো, ছিল বেড়াল, হয়ে গেল কম্পিউটার গোছের একটা কথা। যে গল্পটা বলতে চলেছি সেটাকে বিজ্ঞান তো দূরের কথা, ইতিহাস বলেই হয়তো কেউ স্বীকার করতে চাইবেন না, এমনই অসম্ভব শুনতে লাগবে ব্যাপারটা। কারণ ভবিষ্যতের কম্পিউটার বানানোর জন্য আমরা ব্যবহার করতে চলেছি এমন এক তত্ত্ব যার সম্পর্কে বিজ্ঞানী মারে গেলম্যান বলেছেন, “এই অদ্ভুত রহস্যময় তত্ত্ব আমরা বুঝি না কিন্তু একে ব্যবহার করতে জানি”।

এই তত্ত্বের সিদ্ধান্তগুলো শুনলে মনে হবে কোন হাস্যকর রূপকথা। এমনই কাণ্ডজ্ঞানহীন সেসব কথা। কিন্তু সেসব কাণ্ডজ্ঞানহীন ব্যাপারগুলোই আদতে প্রকৃতিতে ঘটে। কেন প্রকৃতি এমন? এর উত্তরে বিজ্ঞানী মিশিও কাকু বলছেন, “…… because nature doesn’t care about our common sense”. সুতরাং তত্ত্বের গভীরতায় হাবুডুবু না খেয়ে আমরা বরং দেখি এ তত্ত্বের প্রয়োগ কেমন করে প্রযুক্তির নতুন দিগন্ত খুলে দেবার স্বপ্ন দেখাচ্ছে।

গল্পটা শুরু করা যাক ১৯০০ সাল থেকে। ১৯০০ সাল থেকে কেন? কারণ ঐ বছরেইতো সেই ঘটনা দুটো ঘটলো যাদের থেকে এই গল্পের সূত্রপাত।

প্রথম, প্যারিসে অনুষ্ঠিত গণিতের আন্তর্জাতিক কংগ্রেস-এ ৮ই আগস্ট প্রদত্ত একটি বক্তৃতায় সেসময়ের অন্যতম শ্রেষ্ঠ গনিতজ্ঞ ডেভিড হিলবার্ট (জন্মসূত্রে খাঁটি জার্মান, নারায়ণ সান্যালের ‘বিশ্বাসঘাতক’ যাঁরা পড়েছেন তাঁরা নিশ্চয়ই চিনতে পারছেন এঁকে) গণিতের কিছু অমীমাংসিত (তখনও অবধি) সমস্যার একটি তালিকা দেন যেগুলি তাঁর মতে বিংশ শতকে গণিত গবেষণার অভিমুখ ঠিক করবে।

দ্বিতীয়, ঐ বছরেই অক্টোবর ও তারপর ডিসেম্বর মাসে পরপর প্রকাশিত হলো আরেক জার্মান পদার্থবিদ ম্যাক্স প্ল্যাঙ্কের দুটি গবেষণাপত্র যথাক্রমে, Uber eineVerbesserung der Wienschen Spectralgleichung এবং Zur Theorie des Gesetzes der Energie Veriteilung im Normalspectrum যা ১৯৬৭ সালে প্রকাশিত Dick ter Haar এর The Old Quantum Theory বইতে অনূদিত হয়েছে যথাক্রমে, On an Improvement of Wien’s Equation for the Spectrum ও On the Theory of Energy Distribution Law of Normal Spectrum নামে। এই গবেষণাপত্র দুটি থেকেই সূচনা হলো কোয়ান্টাম তত্ত্ব নামে বিজ্ঞানের সেই বিশেষ শাখাটির যা পরবর্তী শতাব্দীতে (এমনকি এখনো) বিশ্বের সেরা বিজ্ঞানীদের রাতের ঘুম উড়িয়ে দেবে।

কোয়ান্টাম তত্ত্বের মূল বক্তব্যটা অবশ্য খুব সরল। শক্তি তা সে তাপ, আলো যেকোন রূপেই হোক না কেন, তার শোষণ বা বিকিরণ নিরবিচ্ছিন্নভাবে হয় না। হয় ছোট ছোট বিচ্ছিন্ন প্যাকেট রূপে। শক্তির এই প্যাকেটগুলিকেই প্ল্যাঙ্ক নাম দেন কোয়ান্টা। এই কোয়ান্টাগুলিকে কল্পনা করা যেতে পারে শক্তির কণা রূপে। অর্থাৎ তড়িৎচুম্বকীয় তরঙ্গ বলে যাকে এতোদিন ভেবে আসছিলাম তা আসলে নিরবিচ্ছিন্ন তরঙ্গ নয়, অতি ক্ষুদ্র কণার স্রোত। মানে আগের বিজ্ঞানীরা (যেমন র‍্যালে, হাইগেন্স, ম্যাক্সওয়েল) ভুল করেছিলেন, প্ল্যাঙ্ক তাঁদের ভুল শুধরে দিলেন, তাই তো ?

না, ব্যাপারটা এতো সরল নয়। আগের বিজ্ঞানীরা ভুল করেননি! তাঁরা তাঁদের তত্ত্ব দিয়ে বিভিন্ন প্রাকৃতিক ঘটনা যেমন ব্যতিচার (Interference), অপবর্তন (Diffractin), সমবর্তন (Polarization) এসবের সুন্দর ব্যাখা দিতে পেরেছিলেন যেগুলো কিনা ঐ কণা তত্ত্ব বা কোয়ান্টাম তত্ত্ব দিয়ে ব্যাখা করা যায় না। কিন্তু আবার অন্য কিছু ঘটনা যেমন, কৃষ্ণবস্তু বিকিরণ (Blackbody radiation) বা আলোকতড়িৎ ক্রিয়া (Photo-Electric Effect) এসবের ব্যাখা তরঙ্গতত্ত্ব ব্যবহার করে দেওয়া যায় না।

শুরু হলো বিজ্ঞানের জগতে প্রথম প্রলয়। বিজ্ঞান মেনে নিতে বাধ্য হল যে দুটি পরস্পরবিরোধী তত্ত্বের দুটিই ঠিক। শক্তি কণাও বটে আবার তরঙ্গও বটে। কখন কি রূপে তাকে দেখবো তা নির্ভর করছে কি ধরনের ঘটনা বা পরীক্ষার মাধ্যমে তার স্বরূপ বোঝার চেষ্টা করছি তার ওপর।

কিন্তু এখানে শেষ নয়, বরং এখান থেকে শুরু চিন্তা ও যুক্তির জগতে মহাপ্রলয়ের। ঐ যে বলেছিলাম, প্রকৃতি আমাদের যুক্তি বা কাণ্ডজ্ঞানের তোয়াক্কাই করে না! কিছু বিজ্ঞানীর এবারে মনে হল, শক্তি যদি কণারূপে থাকতে পারে তাহলে পদার্থকণা যেমন ইলেক্ট্রন, প্রোটন এদেরও কি তাহলে তরঙ্গধর্ম আছে? উপযুক্ত পরীক্ষার মাধ্যমে কি তা বোঝা যাবে? উত্তর পাওয়া গেল, হ্যাঁ আছে এবং হ্যাঁ বোঝা যাবে।

১৯২৩ সালের সেপ্টেম্বর মাসে লুই ডি ব্রগলি কণা-তরঙ্গ দ্বৈত ধর্ম (wave particle duality) বিষয়ে গবেষণাপত্র লিখে ফেলেছেন যেখানে তিনি ইলেক্ট্রন তরঙ্গের তরঙ্গদৈর্ঘ্য বিষয়ে কিছু আলোকপাত করেছেন। যার জন্য পরের বছর ১৯২৪ সালে তিনি ডক্টরেট উপাধি পান এবং পরে নোবেল সম্মানেও ভূষিত হন।

১৯২৭ সালের জানুয়ারীতে ক্লিন্টন ডেভিসন এবং লেস্টার জার্মার একটি পরীক্ষার মাধ্যমে দেখান ইলেক্ট্রনের আলোর মতোই অপবর্তন হয় সুতরাং ইলেক্ট্রনের নিশ্চিত রূপে তরঙ্গ ধর্ম আছে। ঐ বছরই নভেম্বর মাসে জর্জ পাজেট থমসন একটি ভিন্নধর্মী পরীক্ষার মাধ্যমে আবার ইলেকট্রনের অপবর্তন প্রমাণ করেন। এই আবিষ্কারের জন্য ডেভিসন ও থমসন ১৯৩৭ সালে নোবেল সম্মান পান। প্রসঙ্গত উল্লেখ্য, জি পি থমসনের বাবা স্যার জোসেফ জন (জে জে) থমসন ১৯০৬ সালে নোবেল পুরষ্কার পেয়েছিলেন ইলেকট্রন ‘কণা’ আবিষ্কারের জন্য।

অবশ্য এসবের আগেই ১৯২৬ সালের মার্চ মাসে এরউইন শ্রোয়েডিঙ্গার এমন দ্বৈত ধর্ম বিশিষ্ট কণা বা তরঙ্গের গতিপ্রকৃতি বা গতিবিদ্যা বর্ণনা করার জন্য তৈরি করে ফেলেছেন তরঙ্গ বলবিদ্যা বা ওয়েভ মেকানিক্স। পরের মাসেই তরুণ হাইজেনবার্গ দিলেন ম্যাট্রিক্স মেকানিক্স। পদার্থবিদ্যার বসন্তকাল! সব ফুল যখন একসঙ্গে ফুটতে শুরু করেছে। কিন্তু শ্রোয়েডিঙ্গারের এই তরঙ্গ বলবিদ্যার মূল ভিত্তি যেটি সেই শ্রোয়েডিঙ্গার সমীকরণের মধ্যে ψ(সাই) নামে একটি চলরাশি উপস্থিত ছিল যা নিয়ে এল সুপারপজিসন প্রিন্সিপল নামে এমন একটি ধারণা যাকে স্বয়ং শ্রোয়েডিঙ্গার মেনে নিতে পারেননি।

শ্রয়েডিংগার

কেন? কি এই সুপারপজিসন প্রিন্সিপল? খুব সহজ ভাষায় বললে এটি বলছে, কোন কণা বা সিস্টেম একইসময়ে, একসঙ্গে তার জন্য নির্দিষ্ট সবকটি সম্ভাব্য অবস্থায় বা State এ থাকে। তো এতে সমস্যা কেন? কারণটা শ্রয়েডিংগার নিজেই ব্যাখা করেছেন তাঁর বিখ্যাত মানসিক পরীক্ষা বা থট এক্সপেরিমেন্ট, বেড়ালের পরীক্ষা বা ক্যাট এক্সপেরিমেন্ট এর মাধ্যমে।

ধরা যাক, একটা বন্ধ বাক্সের মধ্যে একটা জীবন্ত বেড়াল আছে এবং তার সঙ্গেই এমন একটা যান্ত্রিক ব্যবস্থা (যেটা বেড়ালটা ছুঁতে পারবে না) যেখানে একটা পাত্রে সামান্য তেজস্ক্রিয় পদার্থ আছে। এতই কম যে, এক ঘন্টায় একটা পরমাণূ ভাঙ্গতে পারে (৫০% সম্ভাবনা) বা নাও পারে (৫০% সম্ভাবনা)। যদি পরমাণু ভাঙে তাহলে ঐ যান্ত্রিক ব্যবস্থা বেড়ালটাকে মেরে ফেলবে (একটা বন্দুক চলবে বা একটা বিষাক্ত গ্যাস বেরোবে) কিন্তু পরমাণু না ভাঙলে কিছুই হবে না, বেড়ালটা বেঁচে থাকবে। এখন এই বন্ধ বাক্সটাকে যদি একঘন্টা ফেলে রাখা হয় তাহলে সেই একঘন্টার মধ্যে বেড়াল্টার কি হবে? সে বেঁচে আছে না মারা গেছে?

সাধারণ বুদ্ধি বলে বেড়ালটা হয় বেঁচে আছে না হলে মারা গেছে – যেকোন একটা ঘটেছে। কিন্তু না, সুপারপজিসন প্রিন্সিপল বলছে, না, বেড়ালটা একইসঙ্গে মরে গেছে, আবার বেঁচেও আছে!! মানে জীবন্ত বেড়াল আর মৃত বেড়ালের একটা সুপারপজিসন অবস্থা হয়ে আছে বাক্সের ভেতর। তার মানে কি একটা বেড়াল দুটো বেড়াল হয়ে গেছে বাক্সের ভেতর? হ্যাঁ তাই হয়েছে!! তার মানে এবার বাক্স খুললে দুটো বেড়াল দেখতে পাবো? না, তা কিন্তু পাবো না, কারণ দেখা মানেই সিস্টেমের ওপর প্রভাব বিস্তার করা এবং সেই বহিঃস্থ প্রভাবের কারণে ঐ সিস্টেমের সুপারপজিসন অবস্থা বা State নষ্ট হয়ে যাবে (কোয়ান্টাম বলবিদ্যার ভাষায় Collapsing of psi function), ফলে দেখতে পাবো একটাই বেড়াল, জীবিত বা মৃত।

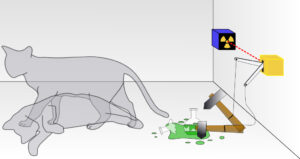
জীবন্ত বেড়াল আর মৃত বেড়ালের একটা সুপারপজিসন অবস্থা হয়ে আছে বাক্সের ভেতর

অসম্ভব মনে হচ্ছে? পাগলের প্রলাপ মনে হচ্ছে? তাহলে বিশ্বসেরা বিজ্ঞানীদের বিনিদ্র রজনীর জগতে আপনাকে স্বাগত। আপনিও তাঁদের মতোই কোয়ান্টাম বলবিদ্যা বুঝতে (মানে না বুঝতে) শুরু করেছেন। কি বলছেন? এসব শুধু গাণিতিক সম্ভাবনা, বাস্তবে এমন অদ্ভুত অসম্ভব ঘটনা ঘটতেই পারে না? যদি বলি, পারে!! এমন অদ্ভুত অসম্ভব ঘটনাই বাস্তবে ঘটে। বারংবার বিভিন্ন ভাবে বিভিন্ন রকম পরীক্ষায় দেখা গেছে অদ্ভুত অসম্ভব ঘটনাটাই বাস্তবে ঘটে। স্থানাভাবে আমরা এখানে সেসব আর বর্ণনা করলাম না, আপাতত মেনে নিন যে সুপারপজিসন প্রিন্সিপল একটা বাস্তব সত্য, একে আমরা বুঝতে না পারলেও ব্যবহার করতে জানি। একটু পরেই তা আমরা দেখবো। আপাতত পদার্থবিদদের ছেড়ে চলুন গণিতজ্ঞদের ও তাঁদের সমস্যার সঙ্গে একটু পরিচয় করে আসি।

কোথায়? কবে?

ঐ যে আগেই বলেছি, ১৯০০ সালের সেই বিশেষ মুহুর্তে যখন ডেভিড হিলবার্ট গণিত জগতের সামনে তুলে ধরছেন তেইশটি অমীমাংসিত সমস্যার সেই তালিকাটি।

ডেভিড হিলবার্ট

সেই তালিকার ২য় ও ১০ম সমস্যাদুটি ছিল গণিত বা যে কোনো ফর্মাল সিস্টেমের নিজস্ব চরিত্র বিষয়ে। দুটি সমস্যা একত্রে নিলে পাওয়া যায় তিনটি প্রশ্ন;

১) গণিত বা ফর্মাল লজিক বা যুক্তিবিজ্ঞান কি সম্পূর্ণ (Complete)?

সম্পূর্ণতা বলতে বোঝায় সেই সিস্টেমের স্বতঃসিদ্ধ ও যুক্তি বাক্য ব্যবহার করে সব সত্য উক্তি (True statement) প্রমাণ করা যায়।

২) গণিত বা ফর্মাল লজিক বা যুক্তিবিজ্ঞান কি সঙ্গতিপূর্ণ (Consistent)?

সঙ্গতিপূর্ণ বলতে বোঝায় সেই সিস্টেমের স্বতঃসিদ্ধ ও যুক্তি বাক্য ব্যবহার করে কোনো মিথ্যা উক্তি (False statement) প্রমাণ করা যাবে না।

৩) গণিত বা লজিকের সব উক্তি কি নিষ্পত্তিযোগ্য (Decidable)?

নিষ্পত্তিযোগ্য বলতে বোঝায়, এমন কোনো যান্ত্রিক পদ্ধতি কি আছে যা সব যুক্তিসঙ্গত প্রশ্নের ‘হ্যাঁ’ বা ‘না’ তে উত্তর দিতে পারবে?

১৯০০ সালে হিলবার্ট বলেছিলেন যে এ প্রশ্নগুলোর উত্তর তাঁর জানা নেই কিন্তু তাঁর বিশ্বাস এগুলোর উত্তর হ্যা-বাচক। দুঃখের বিষয় ১৯৩৬-৩৭ সালে দুজন অসাধারণ গণিতজ্ঞ কার্ট গ্যেডেল ও অ্যালান টুরিং আলাদাভাবে প্রমাণ করে দিলেন তিনটি প্রশ্নেরই উত্তর হলো “না”।

এরমধ্যে প্রথম দুটি প্রশ্ন ওতপ্রোতভাবে জড়িত, গ্যেডেল দেখালেন কোনো ফর্মাল সিস্টেম একইসঙ্গে সম্পূর্ণ ও সঙ্গতিপূর্ণ হতে পারে না। একটু সহজ উদাহরণ থেকে বুঝে নিই ব্যাপারটা? ধরুন নিচের বাক্যটি,

‘এই বাক্যটি প্রমাণ করা সম্ভব নয়’

যদি কোনো সিস্টেম এটি প্রমাণ করতে পারে তাহলে বাক্যটি হয় মিথ্যা এবং তখন সিস্টেমটি হয়ে যাবে অসঙ্গত কারণ একটি মিথ্যা বাক্য প্রমান হয়ে গেছে। আর যদি প্রমাণ না করা যায় তাহলে বাক্যটি সত্য হবে বটে কিন্তু সিস্টেম হয়ে যাবে অসম্পূর্ণ কারণ সত্য বাক্য প্রমান করা যাচ্ছে না।

দেখা যাক টুরিং কেমন করে ঐ ৩য় প্রশ্নের উত্তর দিলেন। ৩য় প্রশ্নটি হিলবার্ট ও উইলহেম অ্যাকেরম্যান আরেকটু ফর্মাল আকারে একটি গবেষণাপত্রে প্রকাশ করেন যেখানে এই সমস্যার নাম দেওয়া হয় Entscheidungsproblem বা decision problem। টুরিং এর গবেষণাপত্রের নামও ছিল, On Computable Numbers with an application to Entscheidungsproblem।

অ্যালান টুরিং

হিলবার্টের উদ্ধৃত ঐ “যান্ত্রিক পদ্ধতি” শব্দবন্ধকে বোধহয় টুরিং আক্ষরিক অর্থে নিয়েছিলেন তাই তিনি এমন একটি যন্ত্রের ধারণা তৈরি করলেন যা মানুষের সমস্যা সমাধানের পদ্ধতিকে নকল করতে পারে। গনিতজ্ঞরা সমস্যা সমাধানের জন্য চারটি কাজ করেন। এই কাল্পনিক যন্ত্রটিও তাই করে।

প্রথমত, গনিতজ্ঞরা কিছু নির্দিষ্ট নিয়ম ব্যবহার করে একটি গাণিতিক অবস্থাকে অন্য একটি গাণিতিক অবস্থায় নিয়ে যান। সুতরাং টুরিং এর মেশিন কিছু নিয়মের ভিত্তিতে এক অবস্থা (State) থেকে অন্য অবস্থায় যায়।

২য়ত, প্রতিটি গাণিতিক চিহ্ন, সংকেত ও বর্ণ এখানে সমতুল্য ০ বা ১ এর সারি দিয়ে বোঝানো হয়।

৩য়ত, গনিতজ্ঞরা যেমন খাতায় সংকেত চিহ্ন ইত্যাদি লিখে রাখেন এখানেও তেমনই লেখা ব্যবস্থা আছে, পার্থক্য এই যে এখানে লেখার জায়গাটা খাতার পাতার মতো দ্বিমাত্রিক নয়, একটা সরু কাগজের ফালি বা strip এর মতো একমাত্রিক টেপ।

অন্তিমে, গনিতজ্ঞরা যেমন পুরন লেখায় ফিরে যেতে পারেন ও সেগুলো সংশোধন করতে পারেন তেমনই টুরিং এর মেশিনে একটি পড়া-লেখা কলম বা Read-Write Head আছে যা ঐ টেপ থেকে কিছু পড়তে পারে, নতুন লিখতে পারে বা পুরনো লেখা মুছে দিতে পারে এবং সামনে বা পেছনে যেতে পারে। পুরো জিনিসটা দেখতে হবে এইরকম,

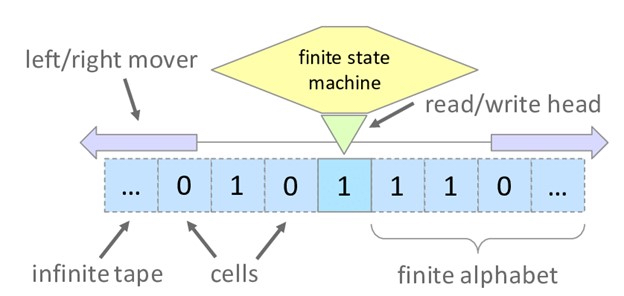
এই সরল দেখতে বিমূর্ত যন্ত্রটি আসলে একটি অতি শক্তিশালী প্রমাণ পদ্ধতি তা বোঝা গেল যখন টুরিং দেখালেন যে গণিত বা যুক্তিবিজ্ঞানের যেকোনো সমস্যা তা সে যতই কঠিন হোক তার জন্ন একটা টুরিং মেশিন মডেল বানানো সম্ভব। সুতরাং এটি এমন একটি যন্ত্রের সরলীকৃত মডেল যা সব গাণিতিক ও লজিকাল সমস্যা compute করতে পারে। কিন্তু এমন শক্তিশালী যান্ত্রিক পদ্ধতিও সব সমস্যার সমাধান করতে পারেনা। টুরিং দেখালেন এমন কিছু সমস্যা আছেই যা computable অর্থাত গণনযোগ্য কিন্তু decidable বা সমাধানযোগ্য নয়। অর্থাৎ টুরিং মেশিন সেইসব প্রশ্নের উত্তর ‘হ্যাঁ’ বা ‘না’ তে দিতে পারবে না।

কেমন হয় সেসব সমস্যা? একটা সহজ উদাহরণ দেখা যাক, ধরুন বিশেষ সংখ্যা বা এমন সংখ্যা যার অঙ্কগুলোর ফ্যাক্টরিয়ালের যোগফলের সমান। কোনো সংখ্যার ফ্যাক্টরিয়াল মানে ১ থেকে ঐ সংখ্যা অবধি যত সংখ্যা আছে সেগুল পরপর গুণ করলে যা হয় তাই। যেমন ৩ এর ফ্যাক্টরিয়াল হলো, ১X২X৩=৬, একে লেখা হয়, ৩! বলে। মানে বিশেষ সংখ্যা-র একটি উদাহরণ হল, ১৪৫ কারণ ১!+৪!+৫!=১৪৫। এবার যদি কোনো টুরিং মেশিনকে প্রশ্ন করা হয়, ৫০০০০ এর চেয়ে বেশী কোন বিশেষ সংখ্যা আছে কি? তাহলে টুরিং মেশিন কিভাবে এর সমাধান করবে? তাকে ৫০০০০ এর বেশী প্রতিটি সংখ্যা পরীক্ষা করতে হবে যতক্ষণ না সে একটা বিশেষ সংখ্যা পায়, কিন্তু যদি ৫০০০০ এর অপরে কোনো বিশেষ সংখ্যা না থাকে? তাহলে কিন্তু টুরিং মেশিন ‘না’ উত্তরটা দিতে পারবে না, কারণ সে পরীক্ষা বা গণনা থামাতেই পারবে না। সুতরাং এটি একটি অসমাধানযোগ্য সমস্যা।

টুরিং মেশিন মডেল থেকে যদিও পরবর্তীকালে কম্পিউটার নামক যন্ত্র তৈরির রাস্তা খুলে গেল এবং টুরিং মেশিন মডেলের মতোই অ্যালেনজো চার্চের ল্যাম্বডা ক্যালকুলাস মডেল ও অবশ্য একই রকম কাজ করে। এই দুটি যৌথ কাজ থেকে পাওয়া গেল চার্চ-টুরিং থিসিস যা বলে, Any effectively computable function can be computed by a Turing machine.

আলোনজো চার্চ 

কিন্তু এতো গেল বিমূর্ত গণিতের কথা, বাস্তব জগতে গণনা-এর জন্য আরো কিছু বিষয়েতো ভাবতে হয়। তথ্যধারক বা Memory, গণনাকার্যে প্রয়োজনীয় সময় ইত্যাদি। তত্ত্বগত ভাবে কোনো সমস্যার সমাধান সম্ভব হলেও যদি সেটি করতে অনেক বছর (ধরুন ৫০০০) লাগে তাহলে লাভ কি? সুতরাং ভাবনা-চিন্তা শুরু হলো ভৌতসংস্থান বা physical resource এর ব্যবহার কমানোর।

এখান থেকেই শুরু কম্পিউটার ও পদার্থবিজ্ঞানের মধ্যে যোগাযোগের। ১৯৮০ এর দশক থেকেই কিছু ব্যতিক্রমী গবেষক ভাবতে শুরু করেছিলেন টুরিং মেশিন নামক বিমূর্ত মডেলটি পদার্থবিদ্যার নিয়মগুলোর সঙ্গে সঙ্গতিপূর্ণ কিনা। এদের মধ্যে কোনো যোগাযোগ আছে কি না? টুরিং এর সময়ে এসব নিয়ে কেউ ভাবেনি কারণ সেসম্য সব গণনাযন্ত্র বা কম্পিউটার কোয়ান্টাম সিস্টেমের চেয়ে অনেক ওপরে মানে ম্যাক্রো স্তরে কাজ করত তাই প্রশ্নটাই অবৈধ ছিল। কিন্তু প্রযুক্তির উন্নতির সঙ্গে সঙ্গে যখন কম্পিউটার ক্ষুদ্র থেকে ক্ষুদ্রতর হতে শুরু করলো তখন এ প্রশ্ন ক্রমশ যুক্তিযুক্ত এমনকি প্রয়োজনীয় মনে হতে লাগলো। ক্ষুদ্র, অতিক্ষুদ্র কম্পিউটার সিস্টেমের ধর্ম বোঝার জন্য তখন বিজ্ঞানীরা তাকালেন সেই অর্ধশতাব্দী আগে আবিষ্কৃত ক্ষুদ্রাতিক্ষুদ্র পদার্থের ধর্ম বিষয়ক বিজ্ঞান কোয়ান্টাম বলবিদ্যার দিকে। অর্ধশতাব্দী প্রাচীন কিন্তু এযাবৎ কাল অবধি পরস্পরবিচ্ছিন্ন দুটি বিষয়ের মধ্যে স্থাপিত হলো যোগসূত্র। কম্পিউটার বিজ্ঞানের গবেষণা এমনকি তাত্ত্বিক বিশ্লেষণে ব্যবহৃত হতে লাগলো কোয়ান্টাম এনট্যাঙ্গলমেন্ট, সুপারপজিসন প্রিন্সিপল এর মতো ধারণা।

কোয়ান্টাম বলবিদ্যার সগে কম্পিউটারের সম্পর্কের কথা প্রথম বলেন ক্যালিফোর্ণিয়া ইনস্টিটিউট অব টেকনোলজির প্রফেসর রিচার্ড ফাইনম্যান ১৯৮২ সালে প্রকাশিত একটি গবেষণাপত্র ‘Simulating Physics with Computers’ এ। এখানে তিনি দেখান কোনো কোয়ান্টাম ঘটনা সিমুলেট করতে মানে কম্পিউটার মডেল তৈরী করতে কোনো ক্লাসিকাল কম্পিউটারের অসম্ভব বেশি সময় লেগে যাবে, কিন্তু কোনো কোয়ান্টাম সিমুলেটর অতি সহজেই কম সময়ে এটা করে ফেলতে পারবে। কিন্তু যেহেতু তিনি এই কোয়ান্টাম সিমুলেটর বস্তুটার কোনো ডিজাইন বা প্রায়োগিক নির্মাণকৌশল বলেননি তাই এটি বেশি লোকের উৎসাহ জাগাতে পারেনি। পরে অবশ্য ফাইনম্যান তাঁর বই ‘Feynman Lectures on Computation’ এ বিশদে আলোচনা করেন কিন্তু এটি প্রকাশিত হয়েছিল তাঁর মৃত্যুর (১৯৮৮) অনেক পরে ১৯৯৬ সালে।

এর আগেই ১৯৮০ সালে অবশ্য পল বেনিওফ নামে এক বিজ্ঞানী রিভার্সেবল টুরিং মেশিনের একটা ডিজাইন দিয়েছিলেন যেখানে দুটো কম্পিউটেশনের মধ্যবর্তী সময়ে মেশিনটা একটা কোয়ান্টাম স্টেট বা অবস্থায় থাকে। কিন্তু প্রতিটি কম্পিউটেশনের সময় যেহেতু মেশিনটা ক্লাসিকাল অবস্থায় ফিরে আসে তাই একে ঠিক ঠিক কোয়ান্টাম টুরিং মেশিন বলা যায় না।

প্রফেসর রিচার্ড ফাইনম্যান

সত্যিকারের কোয়ান্টাম কম্পিউটারের ধারণা দেন অক্সফোর্ড বিশ্ববিদ্যালয়ের ডেভিড ডয়েশ ১৯৮৫ সালে প্রকাশিত তাঁর গবেষণাপত্র “Quantum Theory, The Church-Turing Principle and the Universal Quantum Computer” এ । এখানে তিনি দেখান যে এমন টুরিং মেশিন তৈরী করা সম্ভব যার প্রতিটি কাজ কোয়ান্টাম বলবিদ্যা নির্ধারিত উপায়ে হতে পারে। এবং সেই মেশিনের স্মৃতিধারক টেপে কোনো তথ্য ০ বা ১ জাতীয় নির্দিষ্ট মান থাকার পরিবর্তে দুটি বা তার বেশী মান এর সমসত্ত্ব মিশ্রণ বা সুপারপজিসন অবস্থা থাকবে। সুপারপজিসন অবস্থা, মানে সেই শ্রয়েডিংগারের বেড়াল ! মনে আছে তো? মানে এবার শ্রয়েডিংগারের বেড়াল টুরিং মেশিনের চালিকাশক্তিরূপে ব্যবহৃত।

কিন্তু এতে কম্পিউটেশনের কাজে কী সুবিধা? গাণিতিক জটিলতায় না ঢূকে শুধু এটুকু বলা যাক, কোয়ান্টাম টুরিং মেশিন বা কোয়ান্টাম কম্পিউটার শুধু বেশি শক্তিশালী বা বেশি দ্রুতগতিসম্পন্ন একটা কম্পিউটার মাত্র নয়। এই তত্ত্ব বা তার প্রায়োগিক দিক আদতে কম্পিউটেশনের এক নতুন দিগন্ত খুলে দিয়েছে। কিভাবে? কেন? আসুন সহজ করে সেটা একটু বুঝে নেওয়ার চেষ্টা করা যাক।

প্রথমে একটা হাইড্রোজেন পরমাণুর কথা ভাবি যার একটা মাত্র ইলেকট্রন আছে। প্রতিটি ইলেকট্রনের দুটি সম্ভাব্য অবস্থা আছে, ভূমি অবস্থা (Ground State) আর উত্তেজিত অবস্থা (Exceited State). এবার যদি প্রশ্ন করি ঐ হাইড্রোজেন পরমাণুর ইলেকট্রন কোন অবস্থায় আছে? কি বলবেন? হয় ভূমি নয় উত্তেজিত অবস্থা? কিন্তু সেটা হবে ভুল উত্তর! মনে আছে ঐ বেড়ালের কথা? প্রশ্ন ছিল বেড়ালটা জীবিত না মৃত? উত্তর ছিল, দুটোই। সুপারপজিসন প্রিন্সিপল!! এখানেও উত্তর হবে, দুটোই! ইলেকট্রনটা একইসঙ্গে দুটো অবস্থাতেই আছে। অর্থাৎ ভূমি অবস্থা (ধরি সেটা হলো ০ এর সমতুল্য) আর উত্তেজিত অবস্থা (ধরি সেটা হল ১ এর সমতুল্য)। মানে একটা ইলেকট্রনের তথ্যধারণ ক্ষমতা যদি ১ বিট হয় তাহলে ঐ একটা বিট একইসঙ্গে দুই বিট তথ্য ধরে রেখেছে। যদি এখানে দুটো পরমাণুর কথা ভাবি তাহলে দুটো ইলেকট্রন ০০, ০১, ১০, ১১ এই চাররকম তথ্য ধরে রেখেছে। এবার ভাবুন, বেশি না, ৫০০ টা পরমাণুর কথা, এবার তাহলে তথ্য কতো ধারণ করে আছে ঐ সিস্টেম? সেটা হলো ২^৫০০ বা ১০^১৫০ মানে ১ এর পরে ১৫০ টা শূণ্য বসালে যা হবে সেই সংখ্যাটা। মানে মাত্র ৫০০ বিট জায়গা ব্যবহার করে ২^৫০০ বিট তথ্য রাখতে পারছি! এটাই লাভ?

কিন্তু না, দাঁড়ান। সমস্যা হলো বিটটা মাপতে গেলেই ঐ বাক্স খুলে দেখার মতো অবস্থা হবে। সিস্টেমের সুপারপজিসন অবস্থা বা State নষ্ট হয়ে যাবে (কোয়ান্টাম বলবিদ্যার ভাষায় Collapsing of psi function), ফলে মোট তথ্য সেই ৫০০ বিট এই এসে দাঁড়াবে। তাহলে লাভটা কি? আচ্ছা ভাবুন যদি ঐ দুটো পরমাণূর সিস্টেমের দুটো বিট না মেপে কেবল একটা মানে প্রথমটা মাপি, এবং দেখি সেটার মান ১, তাহলে সঙ্গে সঙ্গে সিস্টেমটা চলে যাবে ১০ ও ১১ এর সুপারপজিসন অবস্থায়। মানে আগের সুপারপজিসন অবস্থা তৎক্ষণাৎ পালটে গিয়ে নতুন সুপারপজিসন অবস্থার জন্ম হবে। এবার যদি ঐ একই কাজ ৫০০ পরমাণুর সিস্টেমটায় করি? ২^৫০০ তথ্য তৎক্ষণাৎ পালটে যাবে। ঠিক যেন প্রকৃতির কাছে ২^৫০০ খানা কাগজ আছে যার প্রতিটায় একটা সংখ্যা লেখা। যেই সিস্টেমটায় কোন পরিবর্তন হল সঙ্গে সঙ্গে প্রকৃতি ঐ ২^৫০০ খানা কাগজ থেকে পুরনো মানটা কেটে নতুন মানটা লিখে দিল।

এবার বলুনতো, এই বিপুল পরিমাণ তথ্য (২^৫০০ মানে গোটা মহাবিশ্বে যত পরমাণু আছে তার চেয়েও বড় একটা সংখ্যা, মহাবিশ্বে মোট পরমাণুর সংখ্যা ১০^৮০ এর মতো) প্রকৃতি রাখলো কোথায়? কীকরেই বা এই বিপুল পরিমাণ তথ্যে মূহুর্তের মধ্যে পরিবর্তন করল? এই অসম্ভব কম্পিউটেশন কিভাবে হল? কোথায় হল? আমরা জানি না! (জানিনা বলা যদিও উচিৎ নয় কারণ ডেভিড ডয়েশ একটা হাইপথেসিস দিয়েছেন কিন্তু সেটা আমরা এখন এই আলোচনা থেকে বাদ রাখছি) কিন্তু আমরা যদি এই কম্পিউটেশনের ক্ষমতাকে ব্যবহার করতে পারি? পারবো? কেন নয়? এই কম্পিউটেশন ক্ষমতা এক ভিন্ন মাত্রার ভিন্ন জগতের কম্পিউটেশন। পরমাণুর নিজস্ব জগত যেখানে চলে কোয়ান্টাম বলবিদ্যার আজব নিয়ম যা আমরা বুঝি না। কিন্তু ঐ যে বলেছিলাম, না বুঝলেও আমরা ব্যবহার করতে জানি। সুতরাং আমরা এখন চলেছি সে নিয়ম ব্যবহার করে প্রযুক্তির ক্ষেত্রে বিপ্লব আনতে। যদিও এখনো আমাদের সাফল্য খুবই সামান্য।

কেন? এই প্রশ্নের উত্তর এই নিবন্ধের আওতার বাইরে। আমরা এখানে বর্ণনা করেছি শতাব্দী ব্যাপী বৃহৎ ধারাবাহিক কর্মকাণ্ডের সামান্য কিছু অংশ। কিভাবে কোয়ান্টাম কম্পিউটেশনের ধারণা গবেষণাপত্র থেকে বাস্তবে আনার চেষ্টা হচ্ছে, তা করতে গিয়ে কি কি সমস্যার সম্মুখীন হতে হচ্ছে, কোয়ান্টাম কম্পিউটেশনের দুর্বলতা ইত্যাদি বহু বিষয়ের আলোচনা বাকী রয়ে গেল। তবে একটা কথা বলে শেষ করি।

কোয়ান্টাম কম্পিউটার তৈরী হওয়া মানে চার্চ-টুরিং থিসিস এর বর্ধিত সংস্করণ যা বলে, “যে সমস্যা কোনো একটি কম্পিউটার যন্ত্রে সমাধান সম্ভব তা অন্য আরেকটি যন্ত্রেও সমাধান সম্ভব এবং প্রয়োজনীয় সময় একে অপরের সমতুল্য” (একটু সরল করে গাণিতিক পরিভাষা বর্জন করে লেখা) তাকে বাতিল করা, কারন দেখা যাচ্ছে কোয়ান্টাম কম্পিউটার এমন কিছু সমস্যার সমাধান করতে পারে যা সাধারণ কম্পিউটার করতে পারবে না।

আর যদি না বানানো যায় কোয়ান্টাম কম্পিউটার? তাহলে বুঝতে হবে কোয়ান্টাম বলবিদ্যার যেসব নিয়মের ভরসায় আমরা এই কম্পিউটার বানানোর কথা ভাবছি তার মধ্যেই কোন ভুল আছে। সেক্ষেত্রে প্রশ্নের মুখে পড়বে কোয়ান্টাম বলবিদ্যা যা প্রায় শত বছর ধরে সব পরীক্ষায় সসম্মানে উত্তীর্ণ হয়েছে।

প্রসঙ্গত বলে রাখি, ২০১৯-এর অক্টোবরে নেচার জার্নালে প্রকাশিত একটি গবেষণাপত্রে গুগুলের কোয়ান্টাম এআই টিম দাবী করেছে যে তারা কোয়ান্টাম কম্পিউটার বানাতে পেরেছে। যদিও এ দাবী নিয়ে অনেকেই সন্দিহান। গুগুলের প্রধান প্রতিদ্বন্দ্বী আইবিএম তো বটেই। এর কারণও আছে, আগেও আরো দুবার গুগুল এমন দাবী করেছিল কিন্তু দুবারই তা ভুল প্রমাণিত হয়েছিল। এবারে অবশ্য নেচার পত্রিকায় বেরোনো প্রবন্ধ, তবু আমিও এখনো অবধি একটু সংশয়ী। দাবী সত্যি হলে মাল্টিভার্স-এর অস্তিত্বও মেনে নিতে হবে কারণ কোয়ান্টাম কম্পিউটারের সঙ্গে ওটাও জড়িত যে। মাল্টিভার্স কী এবং কেন সে নিয়ে আলোচনা এ প্রবন্ধে আর সম্ভব নয়। আপাতত আমরা অপেক্ষায় সম্প্রসারিত চার্চ-টুরিং থিসিস আর কোয়ান্টাম বলবিদ্যা এ দুটোর মধ্যে কোনটা ভুল প্রমাণিত হয় তা দেখার জন্য। আমিতো আমার প্রার্থী বেছে নিয়েছি, আপনারা?

এ প্রবন্ধ লেখার জন্য বেশ কিছু বই (পাঠ্যপুস্তক এবং জনপ্রিয় বিজ্ঞান দু’রকমেরই) এর সাহায্য নিয়েছি। তার ভেতর থেকে কয়েকটি লিখছি। সেগুলো থেকেই উৎসাহী পাঠক আরো সূত্র পাবেন।

1. Quantum, Manjit Kumar; Hachette, India
2. Ultimate zero and one: Computing at Quantum frontier, Collin P. Williams & Scott H. Clearwater; Copernicus
3. Computing with Quantum cats, John Gribbin; Black Swan
4. Minds, Machines and the Multiverse, Julian Brown; Simon & Schuster
5. Quantum Computing for everyone, Chris Bernhardt; The MIT press
6. Quantum Computing and Quantum Information, Michael A. Nielson & Issac L. Chuang; Cambridge University Press
7. Quantum Computing and Communication, Sandor Imre & Ferenc Balazas; John Wiley & Sons
8. Quantum Attacks on Public-Key Cryptosystem, Song Y. Yan; Springer