জ্যামিতির সাথে আমার পরিচয় বহুদিনের। সেই যখন ষষ্ঠ শ্রেণীতে নিরঞ্জন স্যার (আমার অন্যতম প্রিয় শিক্ষকদের মধ্যে একজন) কোণ, রেখা, বৃত্ত, ত্রিভুজ ইত্যাদির সঙ্গে পরিচয় করিয়ে দিলেন। এর সঙ্গেই পরিচয় হলো জ্যামিতির কিছু বিশেষ ধর্মের সঙ্গে। পরবর্তীকালে যেগুলোকে হয় উপপাদ্য অথবা স্বতঃসিদ্ধ বলে জানলাম। তখন অবশ্য জানা ছিল না যে জ্যামিতির ইতিহাস আদতে বুড়ি পৃথিবীর মতই প্রাচীন। সভ্যতার আদিকাল থেকেই নানা প্রাত্যহিক প্রয়োজনে, যেমন গৃহ নির্মাণ, যজ্ঞবেদী নির্মাণ অথবা বন্যার পরে ভূখণ্ডকে পুনর্বিভাজন ইত্যাদি কারণে রেখা কোণ এবং তার বৃত্তীয় পরিমাপ সংক্রান্ত টুকরো টুকরো জ্ঞান জমা পড়ছিল মানব সভ্যতার ভান্ডারে। ত্রিভুজ চতুর্ভুজ ও বৃত্তের কিছু কিছু ধর্ম আবিষ্কৃত ও ব্যবহৃত ছিল। সমকোণ আঁকার পদ্ধতিও অনেক প্রাচীন সভ্যতা বের করে ফেলেছিল। চীন, ভারত মিশর ইত্যাদি সব সভ্যতাতেই জ্যামিতিক জ্ঞানের কিছু ব্যবহার দেখা যায়।

প্রাচীন গ্রীসই যদিও প্রথম জ্যামিতির আবিষ্কারগুলি সূত্রের আকারে বেঁধে ফেলার চেষ্টা করে। প্রায় ৬০০ সাধারণ পূর্বাব্দ নাগাদ পীথাগোরিয়ান সংঘ গণিত কে পূর্ণ সংখ্যা ও ভগ্নাংশের ভিত্তিতে গড়ে তোলার চেষ্টা করে। কিন্তু সে ইমারত গড়ে ওঠার আগেই ভেঙে পড়ে কারণ তাঁরা ইর‍্যাশানাল সংখ্যা ও স্বর্গীয় সংখ্যা (Transcedental numbers) সমূহের কথা ভাবতে পারেননি। কিন্তু এক অদ্ভুত ঘটনার মধ্যে দিয়ে সে সংখ্যা সমূহের অস্তিত্ব সামনে এলো। এটি হয়তো বানানো গল্প হতে পারে কিন্তু এমন গল্প ইতিহাসের কোনো ক্ষতি করেনা বরং তাকে আরো সরস মনোগ্রাহী করে তোলে। সুতরাং গল্পটা বলি।

৪৩০ সাধারণ পূর্বাব্দ নাগাদ এক ভয়াবহ মহামারীর কারণে এথেন্স শহরের জনসংখ্যা প্রায় অর্ধেক হয়ে গিয়েছিল । বলা হয় এসময় শহরের কর্তা ব্যক্তিরা ডেলোসের সূর্য মন্দির অর্থাৎ অ্যাপোলোর মন্দিরের প্রধান পুরোহিতের কাছে যান মহামারী ঠেকানোর উপায় জানতে। অ্যাপোলোর মন্দিরের পুরোহিত হতেন কোনো মহিলা যিনি নাকি ভবিষ্যৎ দেখার ক্ষমতাবতী হতেন দেবতার কৃপায়। তাঁকে বলা হতো অরাকল্ (হ্যাঁ আধুনিক যুগের বিখ্যাত সফটওয়্যার কোম্পানিটির নাম এখান থেকেই অনুপ্রাণিত)। তো সেই অরাকল্ বলেন (অর্থাৎ দেবতা তার মাধ্যমে বলেন, এখনকার দিনে যেমন ঠাকুরের ভর হয় তেমনটা তখনও ছিল আরকি) দেবতার মূর্তির সামনের এক মিটার (মিটার একক তখনকার দিনে ব্যবহৃত হত না, কিন্তু আমরা এখানে আধুনিক একক ব্যবহার করেছি সুবিধার জন্য) দৈর্ঘ্য প্রস্থ ও উচ্চতা বিশিষ্ট বেদীটির দ্বিগুণ আয়তনের একটি বেদী তৈরি করে দেবার জন্য। শহরবাসী উৎসাহের সঙ্গে দুই মিটার দৈর্ঘ্য প্রস্থ ও উচ্চতা বিশিষ্ট একটি বেদী তৈরি করে দেয়। কিন্তু তাতে মহামারী থামে না। তখন সকলে নিজেদের ভুল বুঝতে পারে। না, পাথরের বেদী তৈরি করার সঙ্গে মহামারীর কোনো সম্পর্ক নেই, এ জাতীয় উপলব্ধি নয়। নিতান্তই একটি গাণিতিক সত্য। বেদীর দৈর্ঘ্য প্রস্থ ও উচ্চতা দ্বিগুণ করার ফলে আয়তন দ্বিগুণ হয়নি বরং আটগুণ হয়ে গেছে ! আয়তন দ্বিগুণ করতে গেলে দৈর্ঘ্য প্রস্থ ও উচ্চতা দ্বিগুণ করলে হবে না। তখন দৈর্ঘ্য প্রস্থ ও উচ্চতা যা করতে হবে তা করা এমনকি সংখ্যাটার মান কি হবে তা বার করাই তখন গ্রীকদের পক্ষে সম্ভব ছিল না। কারণ সংখ্যাটা হলো ২ এর কিউবিক রুট বা ত্রিঘাত বীজ। এ সংখ্যাটা একটা ইর‍্যাশানাল সংখ্যা যাকে কোনোভাবেই একটা জ্যামিতিক ছবির মাধ্যমে প্রকাশ করা যায় না। অথচ গ্রীকরা সব সংখ্যাকেই প্রকাশ করতো নির্দিষ্ট দৈর্ঘ্যের রেখার মাধ্যমে। কিন্তু এ ধরনের সংখ্যাকে কিভাবে আঁকা সম্ভব বা প্রকাশ করা সম্ভব তা গ্রীকরা বুঝতে পারছিল না।

৩০০ সাধারণ পূর্বাব্দ নাগাদ ইউক্লিড আবার জ্যামিতির ভিত্তি গড়ে তোলার চেষ্টা করেন এবং সেই সূত্রে পাটীগণিত ও সংখ্যা তত্ত্বের ও। পাটীগণিত ও সংখ্যা তত্ত্ব নিয়ে বরং পরে কখনও আলোচনা করা যাবে। আজ আমরা জ্যামিতি অর্থাৎ কিনা ইউক্লিডীয় জ্যামিতির বিষয়ে কয়েকটি কথা আলোচনা করি।

এ জ্যামিতির নাম ইউক্লিডীয় জ্যামিতি কেন তা সহজবোধ্য। যদিও ইউক্লিডের অনেক আগে থেকেই এ জ্যামিতির মূল প্রতিপাদ্য বিষয় গুলি জানা ছিল কিন্তু তিনিই প্রথম একে কিছু নির্দিষ্ট প্রাথমিক সূত্র, উপপাদ্য বা theorem এবং সেই প্রাথমিক সূত্রের থেকে তার প্রমাণ এই আকারে বেঁধে ফেলেন। গণিতের ভাষায় যাকে বলে formalism বা বিশেষ আকারে সমগ্র শাস্ত্রটির প্রকাশ। সেই প্রায় ২৩০০ বছর আগে থেকে আজ অবধি জ্যামিতির সঙ্গে মানুষের প্রথম পরিচয় হয় ইউক্লিডীয় জ্যামিতি এবং তার সূত্র ও উপপাদ্যের মাধ্যমে। আমার এবং আপনারা যাঁরা এ লেখা পড়ছেন তাঁদের সবার অভিজ্ঞতাই নিঃসন্দেহে একইরকমের সে আমরা ঐ বিশেষ পদ্ধতিটিকে ইউক্লিডীয় বলে জানি আর না জানি।

এ প্রসঙ্গে একটা কথা না বলে পারছি না, বর্তমানে কেউ কেউ বা একটি গোষ্ঠী ইউক্লিডকে এবং তাঁর কাজকে অস্বীকার করতে চাইছেন একথা বলে যে ইউক্লিড একজন কাল্পনিক ব্যক্তি এবং তাঁর কাজ যেগুলোকে বলা হয় সেগুলো পরবর্তী কালের আবিষ্কার। এসবই ইউরোপীয়দের ষড়যন্ত্র ইত্যাদি ইত্যাদি। তার কারণ ইউক্লিডের কাজ সবই পাওয়া গেছে পরবর্তীকালে আরব লেখকদের লেখা বা উল্লেখ থেকে। তাঁর মূল পুঁথি বা manuscript কিছু পাওয়া যায়নি। তাঁর সমসাময়িক কেউ নাকি তাঁর কথা বলেননি। কিন্তু এই অভিযোগ সত্যি নয়। ইউক্লিডের সমসাময়িক লেখকদের যে মূল পুঁথি বা manuscript পাওয়া গেছে সেখানে তাঁর স্পষ্ট উল্লেখ আছে এবং শুধু তাই নয়, সেখানে বহু স্থানে ইউক্লিডের পদ্ধতি অনুকরণ করাও হয়েছে। যাই হোক, ইউক্লিডের ঐতিহাসিকতা প্রমাণ করা এই প্রবন্ধের উদ্দেশ্য নয় সুতরাং তিনি একজন বাস্তব মানুষ এবং তাঁর কাজগুলি আসলে তাঁরই করা এটুকু মেনে নিয়ে আমরা আবার ইউক্লিডীয় জ্যামিতির চর্চাতে ফিরে আসি।

কিন্তু বারবার ইউক্লিডীয় জ্যামিতি কথাটা কেন বলছি? শুধু জ্যামিতি বললেই তো আমার লিখতে এবং আপনাদের পড়তেও সুবিধা, তাই না? তবে কি এর পেছনে কোনো বিশেষ কারণ আছে? হ্যাঁ ঠিকই ধরেছেন, কারণ আছে। কারণটা কী? হ্যাঁ, এবারও ঠিক ধরেছেন; ইউক্লিডীয় জ্যামিতি একমাত্র জ্যামিতি নয়। তাঁর দেখানো রাস্তা বাদেও অন্য রাস্তা আছে যে পথে হেঁটে একটা জ্যামিতিক ইমারত বা formal geometric structure গড়ে তোলা যায়। এবং তা করাও হয়েছে। কিন্তু মজার ব্যাপার হলো সেটা করতে এমনকি বুঝতে পারা গেছে ইউক্লিডীয় জ্যামিতির দেখানো পথে হাঁটতে গিয়েই। কী করে? হ্যাঁ সেই গল্পটাই আজ বলবো। কিন্তু সে গল্পের মজাটা উপভোগ করার জন্য সামান্য একটু ইউক্লিডীয় জ্যামিতির মূল বিষয়ে জানতে হবে।

এবার খুবই সম্ভাবনা পাঠকসংখ্যা শূন্যে নেমে আসার। যাঁরা গণিতে পারদর্শী তাঁরা এবার ঠোঁট উল্টে বলবেন, ” চলি হে, তোমার কাছে আর জ্যামিতি শিখবো না। বরং তোমার দরকার হলে আমাদের কাছে এসো, শিখিয়ে দেবো। ” আর যাঁরা আমার মতো বিশেষ রূপে অজ্ঞ তাঁরা নিশ্চয়ই ব্যাজার মুখে ভাবছেন, ” ধ্যাত্তেরি কি জ্বালা ! এলাম একটু গল্প শুনতে আর এ এখন বলে অঙ্কের ক্লাস করাবে !”

দু-দলকেই বলবো, আপনাদের যুক্তি একশো ছেড়ে দেড়শ শতাংশ ঠিক। কিন্তু একটু শুনেই যান, কথা দিচ্ছি অঙ্ক কম বরং গল্পই বেশি থাকবে। তাহলে শুরু করি, হ্যাঁ?

দু’হাজার বছরের ও বেশি আগে ইউক্লিড একটি কালজয়ী গ্রন্থ রচনা করেন যার নাম এলিমেন্টস। তার পরবর্তী যুগের গ্রীকদের, আরবের গৌরবময় সময়ের এবং ইউরোপের অন্ধকার যুগ পার করে নবজাগরণ যুগের গণিতজ্ঞদেরও প্রেরণাদাতা ছিল এই গ্রন্থটি। কিন্তু কি ছিল এতে, যাতে এ বইটির এতো আদর?

প্রথমত, ইউক্লিডের পূর্বে যত গণিত জানা ছিল, (থেলেস, পীথাগোরীয়ান সম্প্রদায়, ইউডকসাস প্রমুখদের রচিত বা সংকলিত) এটি সে সবকিছুর সংকলন।

২য়ত, এই সমস্ত গণিতের ধারণা ও উপপাদ্য গুলি বিক্ষিপ্ত ও বিচ্ছিন্ন ভাবে ছড়িয়ে ছিল। এই বইতেই প্রথম সেগুলি যুক্তিসম্মতভাবে সাজানো হয় এবং যেখানে সংযোগ নেই সেখানে ইউক্লিড প্রয়োজন মতো উপপাদ্য সৃষ্টি করে সংযোজন করেন।

৩য়ত, উপপাদ্য প্রমাণের আপাত বিচ্ছিন্ন বিষয়গুলি সাজানো হয় এভাবে; যদি উপপাদ্য ‘খ’-এর প্রমাণ উপপাদ্য ‘ক’-এর ওপর নির্ভর করে তাহলে উপপাদ্য ‘ক’ আগে প্রমাণ করা হবে তারপর উপপাদ্য ‘খ’।

৪র্থ এবং সবচেয়ে গুরুত্বপূর্ণ বৈশিষ্ট্য ছিল প্রমাণ পদ্ধতিতে স্বতঃসিদ্ধের প্রয়োগ। যে বৈশিষ্ট্যের চারপাশে আমাদের এ কাহিনী আবর্তিত।

স্বতঃসিদ্ধ কি? স্বতঃসিদ্ধ হলো কতগুলো অসংজ্ঞায়িত বিবৃতি যেগুলোর কোনো প্রমাণ নেই। প্রমাণ ছাড়াই এগুলোকে সত্য বা সঠিক বলে ধরে নিতে হবে। এই বিবৃতিগুলিতে পরিবেশিত বক্তব্যের ওপরেই যুক্তি সাজিয়ে একের পর এক প্রমাণ করা যাবে অন্যান্য উপপাদ্যগুলি। তবে হ্যাঁ, এই স্বতঃসিদ্ধগুলো যেমন তেমন ভাবে নিলেই চলবে না। কয়েকটি শর্ত মানতে হবে – যেমন, এদের কোনো একটাকে অন্যগুলো থেকে প্রমাণ করা যাবে না, কোনোটাই অন্যগুলোর বিরোধী হতে পারবে না ইত্যাদি। প্রথম শর্তটা ভালো করে লক্ষ্য করতে অনুরোধ করবো। এই শর্তটি যদি কোনো স্বতঃসিদ্ধ পালন না করে তাহলেই সেটি আর স্বতঃসিদ্ধ থাকে না, হয়ে যায় উপপাদ্য, অর্থাৎ যেটি অন্য কোনো একটি বা একাধিক স্বতঃসিদ্ধ থেকে অবরোহী যুক্তিসঙ্গত পদ্ধতিতে প্রমাণ করা যায়।

এই দেখুন, আবার একটা নতুন কথা বলে ফেললাম। “অবরোহী যুক্তি” আবার কি? বিশেষ কিছু নয়; অবরোহী যুক্তি মানে যে যুক্তির সাহায্যে সরলতম স্বতঃসিদ্ধ থেকে উপপাদ্য অবধি পৌঁছনো যায়। অর্থাৎ যুক্তির সিঁড়ি বেয়ে সরল থেকে জটিলতার দিকে যাত্রা।

যাই হোক এই পাঁচটি স্বতঃসিদ্ধ হলো,

১) যেকোনো দুটি বিন্দু সংযুক্ত করে একটি সরলরেখা অঙ্কন করা সম্ভব।

২) যেকোনো সীমাবদ্ধ সরলরেখাকে যতটা প্রয়োজন বাড়িয়ে নেওয়া চলে।

৩) যে কোনো একটি বিন্দুকে কেন্দ্র করে যে কোনো ব্যাসার্ধের একটি বৃত্ত অঙ্কন করা যায়।

৪) সমস্ত সমকোণই সমান।

৫) একই সমতলস্থিত দুটি সরলরেখাকে কোনো একটি তৃতীয় সরলরেখা ছেদ করলে যদি এই শেষোক্ত রেখার একই দিকে অবস্থিত অন্তঃকোণ দুটির সমষ্টি দুই সমকোণের কম হয় তাহলে এই দিকে প্রথমোক্ত সরলরেখা দুটিকে যথেষ্ট বর্ধিত করলে সে দুটি পরস্পরকে ছেদ করবে।

দেখাই যাচ্ছে প্রথম চারটি স্বতঃসিদ্ধ যতটা সরল এবং সহজে বোধগম্য শেষোক্তটি অর্থাৎ পঞ্চমটি ঠিক তেমন সরল বা সহজে বোধগম্য নয়। সম্ভবত এটি নিয়ে স্বয়ং ইউক্লিডের মনেও সন্দেহ ছিল যে এটি হয়তো স্বতঃসিদ্ধ নয়, হয়তো এটি একটি উপপাদ‍্য। হয়তো অন‍্য চারটি থেকে এটি প্রমাণ করা সম্ভব।

ইউক্লিড অবশ‍্য নির্দিষ্টভাবে তাঁর এমনতর সন্দেহের কথা কোথাও লিপিবদ্ধ করেননি সুতরাং আপনারা উল্টে আমাকেই ধমকে দিতে পারেন, তুমি কোথাকার জ‍্যোতিষী এলে হে? একেবারে দুহাজার বছর আগের একজনের মনের কথা জেনে বসে আছো!

হ‍্যাঁ অবশ্যই আমি বলতে পারি না ইউক্লিডের মনে কি ছিল। কিন্তু পরবর্তীকালে আরও অন‍্যান‍্য গণিতবিদরা যে এটি নিয়ে সন্দেহ প্রকাশ করেছেন সেটা তো আমরা নিশ্চিতরূপে জানি। আর এই সন্দেহ থেকেই মহাপ্রলয়ের সূত্রপাত।

তবে সে বিষয়ে কথা বলার আগে প্রথম চারটি স্বতঃসিদ্ধ নিয়ে একটু ভেবে নেওয়া যাক। প্রথম দুটি আমাদের অভিজ্ঞতার সঙ্গে ভালো মিলে যায়। কিন্তু তৃতীয়টি একটু গভীর চিন্তা দাবি করে।

তৃতীয়টি আরেকবার লিখি,

যে কোনো একটি বিন্দুকে কেন্দ্র করে যে কোনো ব্যাসার্ধের একটি বৃত্ত অঙ্কন করা যায়।

ভেবে দেখুন, এটি আদতে বলছে যে দেশে (space) দূরত্ব এমনভাবে সংজ্ঞায়িত বা defined যে একটি রেখাংশের দৈর্ঘ্যের কোনো পরিবর্তন হবে না যদি আমরা একে এক জায়গা থেকে অন্য জায়গায় নিয়ে যাই। অর্থাৎ আপনি বৃত্তের কেন্দ্রটি এখানে রাখুন বা চাঁদে, বৃত্তের ব‍্যাসার্ধের পরিবর্তন না করলে বৃত্তটি একই এবং বিপরীতে একই বৃত্তের ব‍্যাসার্ধ সর্বদাই সমান। অন‍্যকথায় এটি আসলে দেশ (space) এর একটি গুরুত্বপূর্ণ বৈশিষ্ট্য দূরত্ব বা দৈর্ঘ্যকে সংজ্ঞায়িত করে।

আসুন চতুর্থ স্বতঃসিদ্ধে, লেখা যাক আরেকবার,

সমস্ত সমকোণই সমান।

এটি প্রাথমিকভাবে খুবই সরল এবং নিশ্চিত বলে মনে হয়; কিন্তু এর গভীরতা বুঝতে গেলে আপনাকে প্রথমে ভাবতে হবে সমকোণের সংজ্ঞা কি? সমকোণ এইভাবে সংজ্ঞায়িত করা যেতে পারে যে এটি এমন কোণ যা আঁকার সময় একটি সরলরেখা অপর একটি কে ছেদ করলে ছেদবিন্দুর দুপাশে যে দুটি কোণ উৎপন্ন হবে সেই দুটি কোণ পরস্পর সমান। আমরা মেপে দেখতে পারি যে সেই কোণের মান ৯০ ডিগ্রী। কিন্তু সবসময়ই যে এমনটাই হবে তা কিন্তু মোটেও সমকোণের সংজ্ঞা থেকে বোঝা যায় না। আমরা এমন একটা জগতের কথা কল্পনা করতেই পারি যেখানে দুটি সরলরেখা কোনো এক বিশেষ বিন্দুতে ছেদ করলে উৎপন্ন সমকোণদুটি ৯০ ডিগ্রী হবে কিন্তু অন্য কোনো বিন্দুতে সমকোণের মান ৯০ ডিগ্রী হবে না! কিন্তু না, চতুর্থ স্বতঃসিদ্ধ নিশ্চিত করে যে এমনটা হবে না। যেকোনো বিন্দুতেই সমকোণ উৎপন্ন হোক না কেন তাদের মান সর্বদা একই হবে অর্থাৎ তারা পরস্পরের সমান। অন্য কথায়, সব সরলরেখা সব জায়গায় একইরকম হবে। একে বলা যায় সরলরেখা যে সর্বদা সোজা হবে তার শর্ত।

এবার ফিরে আসা যাক পঞ্চম স্বতঃসিদ্ধ বিষয়ে। একে নিয়ে সন্দেহ! সন্দেহটা কিন্তু এই নয় যে এটি ঠিক কিনা, বরং এটি প্রমাণ করা যায় কিনা সে নিয়ে। পরবর্তীকালে এর একটি সরলীকৃত সমতুল (equivalent) আবিষ্কার হয়েছে। যেমন প্লেফেয়ারের স্বতঃসিদ্ধ যা আজকাল স্কুলে শেখানো হয়:

কোনো সরলরেখার বহিঃস্থিত কোনো বিন্দু দিয়ে ঐ সরলরেখার সমান্তরাল করে ঐ সমতলে একটি মাত্র সরলরেখা অঙ্কন করা সম্ভব।

এটি স্বতঃসিদ্ধ ৫ এর সমতুল‍্য এই অর্থে যে এদের একটি থেকে অন‍্যটি প্রমাণ করা যায়।

কিন্তু অন্য চারটি স্বতঃসিদ্ধ থেকে কি পঞ্চমটি প্রমাণ করা যায়? যদি যায় তাহলে জ‍্যামিতির মূল ভিত্তি পাঁচটির বদলে চারটি হয়ে যায়। জ‍্যামিতির দুনিয়া এবং সেই সূত্রে আমাদের দুনিয়া একটু সরলতর হয় যদি….. একটা বিরাট বড় ” যদি ” বসে আছে মাঝখানে।

তাহলে দেখা যাক, এটি প্রমাণ করা যায় কিনা অন্য চারটি থেকে?

প্রমাণ করার জন্য দুটো ভিন্ন রাস্তা আছে। এক, প্রত‍্যক্ষ প্রমাণ পদ্ধতি অর্থাৎ অন্য চারটিকে অবলম্বন করে বা ভিত্তি করে অবরোহী যুক্তিপদ্ধতিতে পঞ্চমটিতে পৌঁছনো। যে পদ্ধতিতে চেষ্টা করেছেন প্রাচীন গ্রীক থেকে শুরু করে মধ‍্যযুগের আরব, নবজাগরণ যুগের ইতালীয় ও অন‍্যান‍্য ইউরোপীয় গণিতজ্ঞ এবং আধুনিক যুগেও অনেকেই।

অন্য রাস্তাটি হলো পরোক্ষ পদ্ধতি, এই পদ্ধতিতে প্রমাণিতব‍্যটিকে অস্বীকার করে বা ভুল ধরে নিয়ে কোনো স্ববিরোধ বা contradiction -এ পৌঁছনোর চেষ্টা করা হয়। যদি পৌঁছনো যায় তাহলে প্রমাণ বাক‍্যটি সত‍্য বা সঠিক। Logic এর ভাষায় একে বলে proof by contradiction. মনে করে দেখুন, ছোটবেলায় জ‍্যামিতির ক্লাসে বেশ কয়েকটি উপপাদ‍্য এই পদ্ধতিতে প্রমাণও করেছেন।

তো এই পদ্ধতিতে ধরে নেওয়া হয়েছে, প্রথম চারটি স্বতঃসিদ্ধ ঠিক কিন্তু পঞ্চমটি ভুল। এবার যুক্তির সাহায্যে খুঁজে বার করার চেষ্টা একটি স্ববিরোধ অর্থাৎ এমন একটি বাক্য বা গাণিতিক অবস্থা যেটি এবং তার বিপরীত বাক্য দুটিই সত্যি বলে প্রতিপন্ন হচ্ছে।

এই দুটি পদ্ধতিতেই পঞ্চম স্বতঃসিদ্ধটি প্রমাণ করার চেষ্টা চলেছে বছরের পর বছর। এ প্রচেষ্টার ফলাফল কি হয়েছে তা আমরা আলোচনা করবো। তবে তার আগে দেখানোর চেষ্টা করবো দুরকম পদ্ধতিতে করা এক একটি প্রচেষ্টা, দেখবো সে চেষ্টার ফল এবং তারপর সেই ফলের ভিত্তিতে গড়ে ওঠা সাধারণ সিদ্ধান্তটি জানবো।

এতো কষ্ট না করে মানে জ‍্যামিতিক প্রমাণ পদ্ধতির জটিলতা বা কচকচির মধ্যে না গিয়ে সরাসরি লিখে দেওয়া যেত যে প্রমাণ প্রচেষ্টার ফল কি হয়েছে। কিন্তু বিজ্ঞানের ইতিহাস লেখার সময় আপ্তবাক‍্য বলার মতো করে ঘটনা বর্ণনা না করে বৈজ্ঞানিক পদ্ধতি (অর্থাৎ পরীক্ষা-পর্যবেক্ষণ-সিদ্ধান্ত) অবলম্বন করাই উচিৎ বলে মনে হলো। কেউ যদি গণিতের কথায় আমার মতোই বিরক্তি বোধ করেন তিনি স্বচ্ছন্দে প্রমাণ প্রচেষ্টার বিবরণ বাদ দিয়ে তার পর থেকে ঘটনাসূত্র তুলে নিতে পারেন। কোনো ছন্দপতনের সম্ভাবনা নেই।

সমান্তরাল স্বতঃসিদ্ধ প্রমাণের প্রথম চেষ্টা যিনি করেছিলেন তিনি হলেন টলেমী। যদিও তারপরে প্রক্লুস ডিওডোকাস ভালোভাবে কাজটি করেন, (মানে চেষ্টাটি আর কি) প্রায় পঞ্চম শতকে। প্রক্লুসের প্রমাণটিকে আমরা একটু সহজ উদাহরণের মাধ্যমে বোঝার চেষ্টা করি।

সাদা কাগজের উপর সোজা সোজা লাইন টেনে সেগুলো কে আবার আলাদা আলাদা নাম দেওয়ার চেয়ে বরং শহরের রাস্তা ঘাটের ম্যাপ নিয়ে কাজ করলে সেটা বেশি বোধগম্য হবে। সুতরাং আমরা তাই করি। দক্ষিণ কলকাতায় যাঁরা থাকেন তাঁরা জানেন গড়িয়া থেকে পার্ক সার্কাস অবধি রাস্তাটি ৫ নম্বর রুট আর টালিগঞ্জ থেকে এসপ্ল্যানেড অব্দি রাস্তাটি ৬ নম্বর রুট নামে পরিচিত। এবং এ রাস্তা দুটি মোটামুটি সমান্তরাল। এ দুটিকেই আমরা দুটি সমান্তরাল রেখার প্রতিভূ বলে ধরে নিচ্ছি। 5 নম্বর রুটের ওপর গোলপার্ককে ৬ নম্বর রুটের সাপেক্ষে একটি বহিঃস্থ বিন্দু ধরা যায়। এছাড়া রাস্তা দুটির মধ্যে আর যা কিছু সম্পর্ক আছে সেগুলি আপাতত ভুলে যান। এ দুটি মাঝে মাঝে কোথাও বেঁকে গেছে কিনা, দুটোর মধ্যে দূরত্ব সব সময় সমান কিনা ইত্যাদি ইত্যাদি। এবারে একবার প্লেফেয়ারের স্বতঃসিদ্ধটা মনে করুন

কোনো সরলরেখার বহিঃস্থিত কোনো বিন্দু দিয়ে ঐ সরলরেখার সমান্তরাল করে ঐ সমতলে একটি মাত্র সরলরেখা অঙ্কন করা সম্ভব।

তাহলে আমাদের ছবিটি এর সঙ্গে মেলাবো কেমন করে? আচ্ছা এই ভাবে দেখুন তো লেখা যায় কিনা?

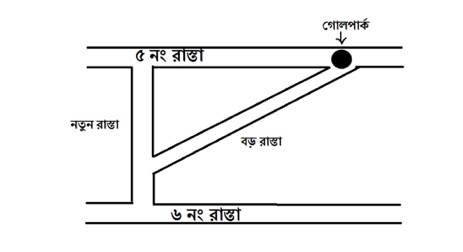
ছ নম্বর রুট এবং ৫ নম্বর রুটের ওপর গোলপার্ক যদি শুধু দেওয়া থাকে তাহলে ৫ নম্বর রুট ছাড়া আর একটিও এমন রাস্তা নেই যেটি গোলপার্কের উপর দিয়ে গেছে আবার ছ নম্বর রুটের সমান্তরাল।

এবার এটি প্রমাণ করতে হলে আমাদের দেখাতে হবে যেকোনো রাস্তা (৫ নম্বর ছাড়া ) যেটি গোলপার্ক হয়ে গেছে সেটি ছ নম্বর রুটকে ছেদ করেছে বা ছ নম্বর রুটে এসে পড়েছে।

ধরা যাক এমন একটি রাস্তা আছে যেটি গোলপার্ক হয়ে গেছে এবং সেটি ৫ নম্বর রাস্তাটি নয়। এই রাস্তাটির আমরা নাম দিলাম “বড় রাস্তা “। আরেকটি রাস্তা আছে যেটি ৫ নম্বর রাস্তার উপর লম্ব অর্থাৎ ৯০ ডিগ্রী কোণে আছে। এই রাস্তার নাম দেওয়া যাক “নতুন রাস্তা “। এই নতুন রাস্তা, বড় রাস্তা আর ৫ নম্বর রাস্তা মিলে একটা সমকোণী ত্রিভুজ তৈরি করে। ( ১ নং ছবি দেখুন ) ধরা যাক আমরা গোলপার্ক থেকে বড় রাস্তা ধরে হেঁটে নতুন রাস্তার সংযোগস্থলে এসে পৌঁছলাম। এবার যতই বড় রাস্তা ধরে হাঁটছি ততই নতুন রাস্তা লম্বভাবে সরে সরে যাচ্ছে অর্থাৎ আমাদের ত্রিভুজটি আকারে বাড়ছে কারণ ঐ নতুন রাস্তা লম্বা হচ্ছে। সঙ্গে নতুন রাস্তা ও বড় রাস্তার সংযোগস্থল ও সরে সরে যাচ্ছে। এবার যেহেতু নতুন রাস্তা ৫ নম্বর রাস্তার সঙ্গে লম্ব সুতরাং এটি বাড়তে বাড়তে একসময় ৬ নম্বর রাস্তাকে ছেদ করবে কিন্তু ঐ ছেদবিন্দুতো বড় রাস্তারও ছেদবিন্দু নতুন রাস্তার সঙ্গে। সুতরাং বড় রাস্তাও ৬ নম্বর রাস্তাকে ছেদ করবে। সুতরাং সমান্তরাল স্বতঃসিদ্ধ প্রমাণিত!

কি? প্রমাণ হলো তো? তার মানে সমান্তরাল স্বতঃসিদ্ধ আসলে একটি উপপাদ‍্য কারণ এটি অন‍্যগুলো থেকেই প্রমাণ করা যায়!

কিন্তু না, একটু দাঁড়ান। নতুন রাস্তা বাড়তে বাড়তে একসময় ৬ নম্বর রাস্তাকে ছেদ করবে তা জানলেন কি করে? এমনতো হতে পারে যে নতুন রাস্তা বাড়ছে কিন্তু কখনোই ৫ ও ৬ নম্বর রাস্তার মধ‍্যবর্তী দূরত্বের সমান হলো না! যেমন, 1/2 + 1/4 + 1/8……. এই অসীম শ্রেণিটির যোগফল কখনও 1 হবে না যদিও এটা বাড়তে থাকবে। কিন্তু এটা অন্য একটা paradox. এটা এখন আমাদের ভাবার বিষয় না। তার চেয়ে বরং ভাবুন, ৫ ও ৬ নম্বর রাস্তার মধ্যে দূরত্ব সর্বদা সব জায়গায় সমান থাকবে এটা জানলেন কেমন করে?

বাঃ, এটা না জানার কি আছে ওরা তো……..। হ‍্যাঁ, হ‍্যাঁ বলুন! ওরা তো সমান্তরাল আর সমান্তরাল সরলরেখার চরিত্র বা ধর্ম যাই বলুন সেটা তো ঐ সব জায়গায় সমদূরত্ব রক্ষা। কিন্তু ভেবে দেখুন সেটাই কিন্তু সমান্তরাল স্বতঃসিদ্ধতে বলা হয়েছে। মানে যেটা আমাদের প্রমাণ করতে হতো সেটাই আমরা প্রমাণে ব‍্যবহার করে বসে আছি।

হ‍্যাঁ প্রক্লুসের প্রমাণের এটাই বড় ভুল। আর এ ভুল তিনি একা করেননি। যত বড় বড় গণিতবিদ এই সমান্তরাল স্বতঃসিদ্ধ বা ইউক্লিডের ৫ম স্বতঃসিদ্ধ প্রমাণ করেছেন বলে মনে করেছেন বা দাবি করেছেন, দেখা গেছে তাঁরা সকলে এই ভুল করেছেন। সে তিনি নবম শতকের আরব গণিতজ্ঞ থাবিত ইবন কুরাহ্ হন বা রেঁনেশা সময়ের গণিতবিদ জন ওয়ালিস হন বা পরবর্তীকালের খ‍্যাতনামা লিঁজান্ড (Legendre)।

এর ফল বহু বিচিত্র রূপে পঞ্চম স্বতঃসিদ্ধের পুনঃপ্রকাশ ; যেমন,

ত্রিভুজের তিনটি কোণের সমষ্টি দুই সমকোণ।

সদৃশ ত্রিভুজের অস্তিত্ব রয়েছে।

একটি সরলরেখার একইদিকে একই দূরত্বে অবস্থিত বিন্দুগুলি একটি সরলরেখা তৈরি করে।

ইত্যাদি ইত্যাদি…..।

এবার আসা যাক দ্বিতীয় পথের পথিকদের কথায়। এঁরা তুলনায় সাহসী কারণ এঁরা ইউক্লিডীয় জ‍্যামিতিকে অস্বীকার করে খুঁজে পেতে চেয়েছেন কোনো একটি স্ববিরোধ। শতকের পর শতক এঁরাও বৃথা খুঁজে ফিরেছেন স্ববিরোধ কিন্তু দেখা গেছে এঁরা যা খুঁজে পেয়েছেন তা আদতে ভিন্নতা, স্ববিরোধ নয়।

একটু খুঁটিয়ে দেখা যাক এঁদের কাজকে। এঁরা প্রধানত দুভাবে অস্বীকার করেছেন সমান্তরাল স্বতঃসিদ্ধকে।

১) একটি বিন্দুর মধ্যে দিয়ে একটি সরলরেখার সমান্তরাল করে কোনো রেখাই আঁকা সম্ভব না। অর্থাৎ যাই আঁকা হোক কোথাও না কোথাও ছেদ করবেই বা অন্য কথায় সমান্তরাল সরলরেখার অস্তিত্বই নেই।

২) কোনো সরলরেখার বহিঃস্থ কোনো বিন্দু দিয়ে ঐ সরলরেখার সমান্তরাল করে একাধিক সরলরেখা আঁকা যায়।

আমাদের স্বাভাবিক ধারণা এবং দর্শনেন্দ্রিয় প্রসূত বাস্তবতার নিরিখে এ দুটোই অস্বাভাবিক কল্পনা, এমনকি কেউ কেউ তো একে পাগলামি বলতেও হয়তো ছাড়বেন না। জগতের ত্রিমাত্রিকতায় বিশ্বাসী ও বসবাসকারী মানবমন স্বভাবতই এখানে স্ববিরোধীতাই আশা করবে।

কিন্তু না, পাওয়া গেল না কোনো স্ববিরোধ! বরং বিভিন্ন সব বিকল্প বাক‍্য প্রমাণ হতে থাকলো যা ইউক্লিডিয় জ‍্যামিতি থেকে ভিন্ন কিন্তু স্ববিরোধী নয়।

এ ব‍্যাপারে সবচেয়ে বেশি উদ‍্যোগী হয়েছিলেন যিনি তিনি ইতালির জেসুইট ধর্মযাজক সাচ্চেরি (১৬৬৭ – ১৭৩৩)। তিনি প্রায় এসে পড়েছিলেন সেই সাফল্যের দোরগোড়ায় যা পরবর্তীকালে অন্য দুজন অখ্যাত গণিতজ্ঞ লাভ করেন।

আরো একজন বিখ্যাত গণিতজ্ঞ একই চিন্তাধারা অনুসরণ করে একই কাজ করে একই সিদ্ধান্তে উপনীত হয়েছিলেন কিন্তু নিজের কাজ প্রকাশ করেননি হাস‍্যস্পদ হওয়ার ভয়ে।

কেন? ইউক্লিডীয় জ‍্যামিতির বাইরে যে আর কিছু থাকতে পারে সেকথা সেসময় লোকে ভাবতেই পারতো না। একে ধরা হতো এক অমোঘ সত‍্য বলে যা দেশ-কালের একমাত্র বিবরণ। ফলে সেই বিখ্যাত গণিতবিদ, তাঁর নামটা বলেই দেওয়া যাক এবার – কার্ল ফ্রেডরিক গাউস, গণিতের রাজপুত্র, কিছুতেই বিজ্ঞানী মহলে হাসির খোরাক এমনকি বিতর্কিতও হতে চাননি। তাঁর আবিষ্কার বছরের পর বছর রয়ে গেছে তাঁর নোটবুকের পাতায় বন্দী।

মজা হলো ঐ দুজন অখ‍্যাত গণিতবিদের কাজ সম্পর্কে গাউস জানতে পেরেছিলেন তাঁর জীবদ্দশাতেই, তবুও প্রকাশ‍্যে তাঁদের স্বীকৃতি জানাতে পারেন নি।

এঁদের একজন, জানুস বোলিয়াই (১৮০২ – ১৮৬০) ছিলেন গাউসের বন্ধুপুত্র। তিনি ১৮২৩ সালেই একটি চিঠিতে নিজের বাবাকে লেখেন নিজের কাজ সম্পর্কে যা তাঁর বাবা উলফগ‍্যাং বোলিয়াই গাউসের কাছে পাঠান বিচারের জন্য। আজকের দিনের ভাষায় peer review এর জন্য। গাউস তাঁকে একটি ব‍্যক্তিগত চিঠিতে অভিনন্দন জানান এবং এও জানান যে এজাতীয় চিন্তা ভাবনা তিনি নিজেও করেছেন।

আমার পূর্বতন একটি লেখায় (কোয়ান্টাম মেকানিকসের ইতিহাস রক্ষণ সংক্রান্ত) এই জানুস বোলিয়াই এর উল্লেখ করেছিলাম হয়তো অনেকের মনে থাকবে। ইনি অখ‍্যাতির মধ্যেই জীবন শেষ করেন।

অন‍্যজন নিকোলাই ইভানোভিচ লোবাচেভস্কি (১৭৯৩ – ১৮৫৬) ঐ ১৮২৩ সালেই একটি রাশিয়ান জার্নাল Kazan Messenger এ নিজের গবেষণাপত্রটি প্রকাশ করেন যেটি ১৮৩৭ সালে সহসা গাউসের দৃষ্টিগোচর হয়। গাউস এঁর জন্য গোটেনজেন এ রয়‍্যাল সোসাইটি অব সায়েন্স এর সদস্য পদ প্রস্তাব করেন এবং সে প্রস্তাবের ফলস্বরূপ লোবাচেভস্কি ১৮৪২ সালে সেখানে সদস‍্যপদ পান। কিন্তু এবারও গাউস প্রকাশ‍্যে এঁর কাজকে স্বীকৃতি দেওয়া থেকে বিরত থাকেন।

কিন্তু ঠিক কি করেছেন এঁরা দুজন? পাঠক লক্ষ্য করবেন, আমি আগে যদিও বলেছিলাম যে স্ববিরোধ সংক্রান্ত একটি প্রমাণ প্রচেষ্টার বিবরণ দেবো কিন্তু দিইনি। দিইনি কারণ গাণিতিক জটিলতা এড়িয়ে এর বিবরণ দেওয়া আমার ক্ষমতার বাইরে। তাই সোজাসুজি বলে দিই যে, এঁরা দুজন প্রমাণ করলেন, কোনো স্ববিরোধে পৌঁছনো সম্ভব না কারণ পঞ্চম স্বতঃসিদ্ধটি স্বনির্ভর (Independent)। একে বাকী চারটি থেকে প্রমাণ বা অপ্রমাণ কোনোটাই করা যাবে না। বস্তুত এটির বিরোধীতা করে যে স্বতঃসিদ্ধগুলি গ্রহণ করা হয়েছে তা থেকে সূচনা হয় নতুন জ‍্যামিতি বা বিকল্প জ‍্যামিতিগুলির।

হ‍্যাঁ বিকল্প জ‍্যামিতিগুলি! একটি নয় বরং দুটি ভিন্ন জ‍্যামিতি সৃষ্টি হয়েছে ঐ দুটি পূর্বলিখিত অস্বীকার দুটি থেকে।

একটি বিন্দুগামী (একই সরলরেখার) একাধিক সমান্তরাল সরলরেখার কল্পনা থেকে সৃষ্টি হলো পরাবৃত্তীয় জ‍্যামিতি।

সমান্তরাল সরলরেখার অনুপস্থিতির কল্পনা থেকে সৃষ্টি হলো উপবৃত্তীয় জ‍্যামিতি।

এর অর্থ হলো দেশ (space) কে আমরা এতোদিন যেমনটা ভেবে আসছিলাম, সমতল (flat), কোনো বক্রতা (curvature) নেই, যেখানে ত্রিভুজের তিনটি কোণ সর্বদা দুই সমকোণ বা 180° হবে, সমান্তরাল সরলরেখাদের মধ্যে দূরত্ব সর্বদা সমান থাকবে, ইত্যাদি আরো আরো ধারণা তা সব এক বিশেষ দেশের বর্ণনা। সেটি ছাড়াও দেশ আরো অন‍্যরকম হতে পারে, বিচিত্র রকম হতে পারে তাদের প্রকৃতি (nature)।

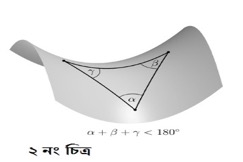
পরাবৃত্তীয় দেশ, যেখানে প্রত‍্যেক ত্রিভুজের তিনটি কোণের সমষ্টি দুই সমকোণ অপেক্ষা ছোট, (২ নং চিত্র ) যেখানে বর্গক্ষেত্র বা আয়তক্ষেত্র জাতীয় চতুর্ভুজ আঁকা যায় না কারণ সেখানে সমকোণই আঁকা যায় না। এ দেশের বক্রতা (curvature) ইউক্লিডীয় দেশের মতো সমতল না বরং পরাবৃত্তীয়। গাণিতিক ভাষায় এর বক্রতা ঋণাত্মক।

অন‍্যদিকে আছে উপবৃত্তীয় দেশ, যেখানে সমান্তরাল সরলরেখাই আঁকা যায় না, ত্রিভুজের তিনটি কোণের সমষ্টি হতে পারে দুই সমকোণের বেশি। এমনকি তিনটি কোণই হতে পারে সমকোণ! এমন দেশের মডেল অবশ‍্য আপনার হাতের কাছেই আছে। এইমুহুর্তে আমরা সবাই বসে আছি তার ওপরে। আজ্ঞে হ‍্যাঁ, আমাদের পৃথিবী! বিশ্বাস হচ্ছে না?

আচ্ছা বেশ একটা গ্লোব হাতে নিন (না থাকলে মনে মনে কল্পনা করলেও চলবে )। এবার উত্তর মেরু থেকে 0° দ্রাঘিমা রেখা বরাবর নিরক্ষরেখা অবধি আসুন একবার। আবার 90° দ্রাঘিমারেখা বরাবর নিরক্ষরেখায় আসুন। দেখুন তো এই দুটো দ্রাঘিমা আর নিরক্ষরেখা একটা ত্রিভুজ সৃষ্টি করলো কিনা? এবার ত্রিভুজের কোণগুলো দেখুন তো প্রতিটাই সমকোণ কিনা? (৩ নং চিত্র ) বিশ্বাস হলো এবার?

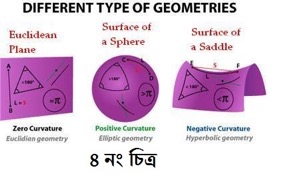
এমন একটা পূর্ণ গোলককে মডেল রূপে ব‍্যবহার করে যদি সৃষ্টি করা হয় উপবৃত্তীয় জ‍্যামিতি তাহলে সেটা হয়ে গেলো দ্বিউপবৃত্তীয় (Double Elliptic) জ‍্যামিতি। আর অর্ধগোলক নিলে সেটা হয়ে যায় একক উপবৃত্তীয় (Single elliptic) জ‍্যামিতি। এ দেশের বক্রতাও (curvature) ইউক্লিডীয় দেশের মতো সমতল না বরং উপবৃত্তীয়। গাণিতিক ভাষায় এর বক্রতা ধনাত্মক। (৪ নং চিত্র দেখুন )

(দেশের গঠন বা space structure নিয়ে আমরা আর বেশি এগোলাম না। যাঁরা আরও গভীরে জানতে ইচ্ছুক তাঁরা তথ‍্যসূত্র 5 ও 6 দেখুন। চিন্তার খোরাক পাবেন, তবে বইদুটি কিন্তু popular science বই না, পাঠ‍্যপুস্তক শ্রেণীভুক্ত)

অর্থাৎ সোজা কথায় সৃষ্টি হলো ইউক্লিডীয় দেশ (space) ব‍্যতিরেকে এক অন্য জগৎ। অন্য দুনিয়া যেখানে ইউক্লিডীয় জ‍্যামিতির নিয়মকানুন অচল। ভেঙে পড়লো ইউক্লিডীয় জ‍্যামিতির সহস্রাব্দী প্রাচীন ইমারত, তার অমোঘতা। ভেঙে পড়লো এই বিশ্বাস যে ইউক্লিডীয় জ‍্যামিতি হলো একমাত্র physics of space বা দেশের পদার্থবিদ‍্যা।

তাহলে কি ইউক্লিডীয় জ্যামিতি অচল হয়ে গেল ? এ দিয়ে যা সব কাজ এতোদিন করছিলাম সেসব কি আর করা যাবে না ? না ব্যাপারটা তেমন ভয়ানক নয়। ইউক্লিডের দেখানো পথে আগেও যেমন আপনার বাড়ির চৌহদ্দি, আপনার জমির পরিমাণ মাপতে পারতেন তেমনটা এখনো পারবেন। ছোটো সমতল ক্ষেত্রের ওপর ইউক্লিডীয় জ্যামিতি আগের মতোই কাজ করবে। কিন্তু যদি গোটা দেশের জমি জরীপ করতে যান তখন ইউক্লিডীয় জ্যামিতি ব্যবহার করলে বড়সড় ভুল বা error দেখা দেবে, কারণ দেশটা কোনো সমতল ক্ষেত্রের ওপর নেই। সেটা একটা বিরাট গোলকের পিঠে আঁকা। মহাজাগতিক সময় ও দুরত্ব মাপার কাজে ইউক্লিডীয় জ্যামিতি ব্যবহার করা যাবে না; তারজন্য অন্যধরনের হিসাবনিকাশ প্রয়োজন।

গাউসের দ্বিধা এবং ভীতির কারণ বোঝা যায়। মানুষের বৌদ্ধিক জগতে এতোবড়ো প্রলয় যে কেউ সহজে মেনে নেবে না তা তিনি বুঝতে পারছিলেন। তিনি নিজেই কি মেনে নিতে পেরেছিলেন? সম্ভবত না, সেজন্যই তো গাণিতিক নির্মাণ সম্পূর্ণ করেও তা বন্দী রেখেছেন ব‍্যক্তিগত নোটবুকের পাতায়। আর বাস্তব জগতে খুঁজে বেড়িয়েছেন এ বিমূর্ত নির্মাণের সমর্থন করতে পারে এমন উদাহরণ, খুঁজেছেন এ তত্ত্বের প্রয়োগক্ষেত্র। তিনটি পর্বতশৃঙ্গের মধ্যের কোণ মাপতে চেষ্টা করেছেন এই আশায় যে হয়তো বৃহৎ ত্রিভুজের ক্ষেত্রে খেটে যাবে অ-ইউক্লিডীয় জ‍্যামিতি, যদিও সাফল্য পাননি।

পরবর্তীকালে অঁরি পঁয়ক‍্যারে বা জর্জ রীম‍্যান আরও এগিয়ে নিয়ে গেলেন এ ধারণাকে। আর তারপর বিংশ শতাব্দীর গোড়ায় এক অসাধারণ প্রতিভা দেখালেন সত্যিই প্রকৃতিবিজ্ঞান বা পদার্থবিদ‍্যায় এ তত্ত্বের প্রয়োগ। গণিতজ্ঞদের বিমূর্ত জগৎ থেকে এ তত্ত্ব এসে পড়লো বাস্তব জগতে। সে প্রতিভা অ‍্যালবার্ট আইনস্টাইন।

কিন্তু সে তো অন্য গল্প। খ‍্যাতির জগৎ থেকে দূরে বসে নিজেদের মনের গহন কোণটিতে অসম্ভবের সাধনা করার সাহস দেখিয়েছিলেন যে দুজন তরুণ তাঁদের প্রতি আমার শ্রদ্ধা নিবেদন করে এখানেই থামলাম আপাতত।

তথ‍্যসূত্র :-

1. Euclid’s Window – Leonard Mlodinow (Penguin publication )

2. The Mathematical Century – Piergiorgio Odifreddi (University Press)

3. গণিতবিকাশের ধারা – অধ্যাপক মনকুমার চক্রবর্তী (পারুল প্রকাশনী)

4. গণিতের ধারাপাত ও গল্পসল্প – মিহির চক্রবর্তী (নান্দীমুখ সংসদ)

5. Geometry : Euclid and beyond – Robin Hartsborne (Springer pubishers)

6. Higher Geometry – F. S. Woods (Ginn and Company )

কভারফোটোঃ রাফায়েল অঙ্কিত “স্কুল অব এথেন্স এ ইউক্লিড” (Internet থেকে প্রাপ্ত, অবাণিজ্যিক ব্যবহার)